Samenvatting
een uiteenzetting voor niet-experts
Computers bewerken gegevens,
maar voor computers maakt het nogal wat uit in welke volgorde deze gegevens behandeld worden.
In dit proefschrift zijn bestaande technieken,
oorspronkelijk bedoeld voor het verdelen van gegevens,
aangepast en uitgebreid zodat zij het herordenen van data mogelijk maken.
Dit herordenen zorgt ervoor dat de nieuwe volgorde van gegevens de computerberekeningen veel sneller maakt.
De oorzaak dat ongestructureerde gegevens het rekenen vertragen ligt bij de architectuur van de computer.
Berekeningen op computers worden gedaan door een processor,
terwijl de gegevens die een computer nodig heeft typisch niet direct op die processor aanwezig zijn;
deze komen van de harde schijf, van compact discs, of van het internet.
Een stukje gegeven dat nodig is om een berekening uit te voeren moet eerst dus een behoorlijke weg naar de processor afleggen.
De infrastructuur die gegevens moeten gebruiken om bij de processor uit te komen,
is de oorzaak dat voor ongestructureerde gegevens de berekeningen langzamer lopen.
We nemen voor het gemak aan dat alle nodige gegevens in het grote interne geheugen (het zogenaamde
Random Access Memory, RAM) van een computer aanwezig zijn.
Tussen de processor van een computer en het interne geheugen,
zijn meerdere steeds kleinere (maar snellere) stukjes geheugen te vinden;
deze worden `caches' genoemd.
Caches worden gebruikt om gegevens die het meest recent nodig waren dichtbij de processor te houden.
Voor gestructureerde problemen levert dit een snelheidswinst op:
als recente gegevens weer nodig zijn kunnen die uit het snelle geheugen worden gehaald,
in plaats van uit het langzamere grotere geheugen.
Echter zijn lang niet alle interessante problemen gestructureerd,
en als er te vaak gerefereerd wordt aan het langzame geheugen,
is de processor langer bezig met wachten op gegevens dan met het daadwerkelijk verwerken van die gegevens.
De oplossing welk wordt gepresenteerd in de eerste twee hoofdstukken,
begint met het analyseren van afhankelijkheid tussen gegevens.
Vervolgens worden gegevens in twee groepen ingedeeld,
zodanig dat de groepen zo min mogelijk van elkaar afhankelijk zijn.
Elk van die twee stukken kan vervolgens recursief op dezelfde manier verder gesplitst worden;
het origineel wordt in twee stukken verdeeld,
die elk wederom gesplitst worden zodat er vier stukken ontstaan,
daarna nogmaals voor acht stukken,
enzovoorts.
Hierop gebaseerd kunnen gegevens geordend worden,
zodanig dat data in kleinere groepen worden behandeld en dus beter in de kleinere caches passen.
De gegevens en de berekening
Het proefschrift behandelt bovenstaande in de context van de
ijle matrix-vector vermenigvuldiging;
dat wil zeggen,
we nemen aan dat de gegevens in de vorm van een matrix gegoten kunnen worden.
Een matrix A van dimensie m×n bevat m maal n stukjes gegevens,
en wordt in het algemeen als een blok weergegeven.
Het volgende is een 2×3 voorbeeldmatrix,
met als type gegevens gewoonweg getallen:
Één getal uit de matrix wordt genoteerd door middel van haar coördinaten:
zo is A
12 gelijk aan √2 en is A
23 gelijk aan 1.
Een matrix waarvan één van de dimensies 1 is,
wordt ook wel een vector genoemd.
Een n ×1 vector is bijvoorbeeld:
Nergens in het proefschrift wordt overigens vereist dat de gegevens getallen
moeten zijn,
in principe zouden gegevens van elke soort behandeld kunnen worden.
Wat wel wordt vereist,
is dat sommatie (+) en vermenigvuldiging (·) tussen twee stukjes gegevens mogelijk is,
en dat er een nul-element bestaat wat niets doet als het ergens bij wordt opgeteld,
en resulteert in het nul-element zelf wanneer het betrokken is bij een vermenigvuldiging
(natuurlijk is dit vanzelfsprekend voor normale getallen,
maar misschien niet voor andere soorten gegevens).
Sommatie en vermenigvuldiging zijn nodig om de
matrix-vector vermenigvuldiging uit te voeren:
voor een matrix A en een vector x als hierboven,
is A maal x (simpelweg genoteerd als Ax) gelijk aan een vector y van dimensie m×1,
met het i-de getal van y gelijk aan de sommatie van elk getal uit de i-de rij van A vermenigvuldigd met het bijbehorende getal uit x.
In wiskundige notatie is dit y
i=∑
j=1,..,nA
ijx
j,
en met het voorbeeld van hierboven krijgen we:
|
y= | ⎛
⎜
⎜
⎝
|
| ⎞
⎟
⎟
⎠
|
| ⎛
⎜
⎜
⎜
⎝
|
| ⎞
⎟
⎟
⎟
⎠
|
= | ⎛
⎜
⎜
⎝
|
| ⎞
⎟
⎟
⎠
|
= | ⎛
⎜
⎜
⎝
|
| ⎞
⎟
⎟
⎠
|
. |
|
Merk op dat x en y niet van dezelfde grootte zijn als A niet vierkant is.
Voor de bovenstaande matrix-vector vermenigvuldiging waren er 6 normale vermenigvuldigingen en 4 sommaties nodig.
Echter zagen we dat er relatief vaak vermenigvuldigd werd met het getal 0,
terwijl de uitkomst daarvan natuurlijk altijd 0 is.
Kijken we dieper dan zien we dat een 0 in A tot gevolg heeft dat het corresponderende element uit x niet wordt bekeken.
Aan de andere kant heeft een 0 in de vector x tot gevolg dat een complete kolom van A wordt genegeerd.
Simpelweg verwijderen van nullen uit x, tezamen met de bijbehorende kolommen uit A, levert dus een directe snelheidswinst.
Het verkrijgen van snelheidswinst uit nullen in A zelf is wat lastiger,
en kan pas worden gedaan wanneer de matrix overwegend uit nullen bestaat,
ofwel,
wanneer de matrix
ijl is.
Dit is precies de situatie waarvoor in dit proefschrift naar een versnelling wordt gezocht,
en verklaart de eerste helft van de titel van het proefschrift:
"
Snelle ijle matrix-vectorvermenigvuldiging...".
Een wiskundige representatie
Alvorens we overgaan tot uitleg van het tweede deel van de titel,
is het eerst noodzakelijk te beschrijven hoe de structuur van niet-nullen kan worden gevangen in een wiskundig model.
Hiervoor worden zogenaamde
hypergrafen gebruikt,
wat een generalisatie is van een normale graaf.
Een graaf is een simpel concept,
en bestaat alleen uit twee ingrediënten:
punten en lijnen,
waar lijnen twee bepaalde punten met elkaar verbinden.
Het treinnetwerk is een simpel voorbeeld van een graaf;
stations kunnen worden weergegeven door punten en sporen tussen verschillende stations door lijnen.
Het hoeft dus zeker niet zo te zijn dat elk punt met elk ander punt is verbonden door een lijn;
het hoeft zelfs niet zo te zijn dat alle punten indirect met elkaar verbonden zijn
(het spoornetwerk van Nederland en van de Verenigde Staten zijn bijvoorbeeld niet verbonden).
Tussen grafen en matrices bestaat al een verband.
Stel bijvoorbeeld dat het Nederlandse spoornetwerk bestaat uit vier stations:
Utrecht, Groningen, Arnhem en Rotterdam.
Qua spoor nemen we aan dat Utrecht verbonden is met alle andere stations,
en dat er voor de rest een directe lijn is van Arnhem naar Groningen.
Deze graaf is weer te geven als een 4×4 matrix met langs elke as de vier stations,
en een 1 in de matrix als er een verbinding is tussen de corresponderende stations:
waar we de diagonaal even laten voor wat het is.
In het geval van een veel groter aantal stations,
is het te verwachten dat de bijbehorende matrix veel nullen gaat bevatten;
ofwel,
de matrix is ijl.
Maar deze representatie stelt nog een andere eis aan de matrix:
hij moet symmetrisch zijn (de linkeronderhoek is gespiegeld gelijk aan de rechterbovenhoek, met de streepjes op de diagonaal als scheiding).
Natuurlijk hebben we liever dat alle ijle matrices goed gerepresenteerd kunnen worden,
en daarom gaan we nu kijken naar de hypergraaf.
Net als een normale graaf,
bevat een hypergraaf punten.
De `lijnen' in een hypergraaf verbinden echter niet twee punten,
maar een arbitraire hoeveelheid punten;
zo een `hyperlijn' wordt ook wel
net genoemd omdat het meerdere punten vangt.
Als we weer als voorbeeld steden als punten in een hypergraaf nemen,
dan kunnen provincies bijvoorbeeld de netten voorstellen.
Een ander voorbeeld is dat we alle steden met een treinstation in een net groeperen,
en evenzo voor steden aan de snelweg, bij vliegvelden, of bereikbaar per bus.
Dit laatste voorbeeld geeft aan dat punten in een hypergraaf in meerdere netten kunnen voorkomen,
naast dat netten meerdere steden kunnen bevatten.
Het geval dat netten onderling nooit dezelfde punten bevatten,
zoals het geval met steden en provincies,
is juist een erg speciaal geval.
Het verband tussen hypergrafen en matrices kan op verschillende manieren worden opgebouwd.
De punten in een hypergraaf kunnen gegeven worden door de kolommen van een ijle matrix,
en de netten corresponderen dan met de rijen van dezelfde matrix:
het net behorende bij rij nummer i verbindt dan de kolommen waar op die rij niet-nullen te vinden zijn.
Zie bij wijze van voorbeeld de volgende illustratie.
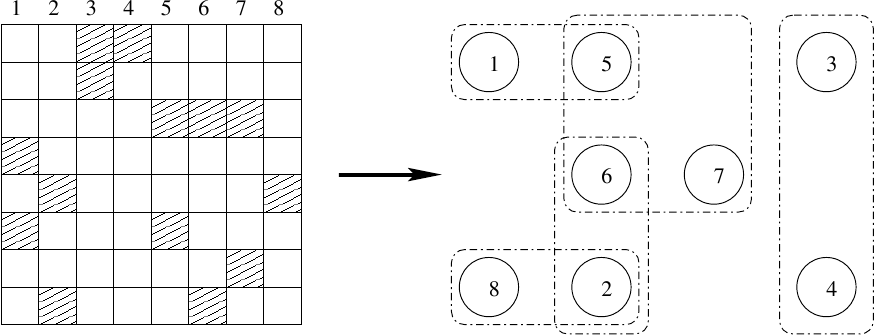
Natuurlijk is het ook mogelijk de rollen van rijen en kolommen om te draaien om zo een andere vertaling mogelijk te maken.
Een hele andere manier is echter om elke niet-nul in de matrix tot een punt in de hypergraaf te benoemen.
Vervolgens maken we twee verschillende groepen netten,
ongeveer zoals we hierboven verschillende netten hadden voor steden met vliegvelden en steden met treinstations:
maar nu voor niet-nullen in een bepaalde rij en niet-nullen in een bepaalde kolom.
Dus als A
ij een niet-nul is in rij i en kolom j,
dan zit deze niet-nul in de netten behorende bij rij i en kolom j:
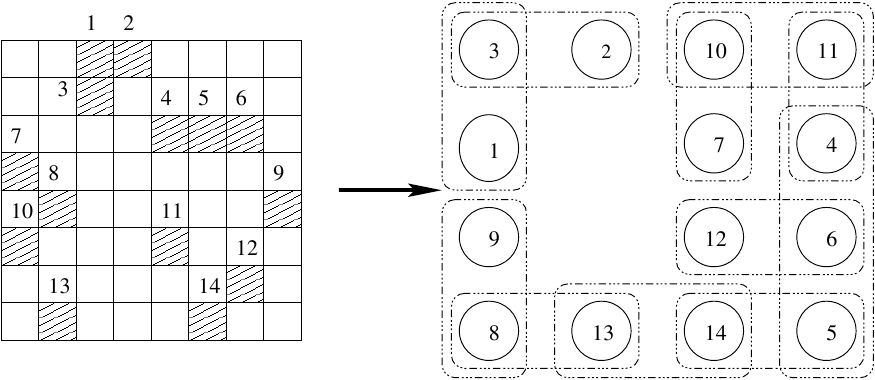
Partitionering van hypergrafen
Nu op naar het tweede deel van de titel: "
...door partitionering en herordening".
Gegeven het voorgaande kunnen we elke ijle matrix omzetten naar een hypergraaf.
Stel dat we de verzameling punten in de hypergraaf opschrijven als
V en de verzameling van alle netten als
N.
Dan wil
partitionering in onze context zeggen dat
V in stukjes wordt opgedeeld.
Natuurlijk kan dit op veel verschillende manieren en moeten we wat eisen opleggen aan de partitionering om er iets van betekenis uit te krijgen.
Daar de punten in
V corresponderen met niet-nullen,
en dus eigenlijk met werk voor de computer,
is de eerste eis standaard dat de stukjes waarin
V wordt opgehakt ongeveer even groot moeten zijn.
Van origine wordt partitionering namelijk gebruikt om parallel rekenen mogelijk te maken;
dat wil zeggen,
het probleem wordt opgedeeld in ongeveer gelijke stukjes die zo min mogelijk met elkaar te maken hebben,
zodat die stukjes zo onafhankelijk mogelijk van elkaar kunnen worden berekend,
en wel op meerdere computers tegelijkertijd.
De tweede eis is dus dat de stukjes onafhankelijk moeten zijn,
en hiervoor gaan we de gegevens van de verschillende netten gebruiken.
Stel dat
V in een arbitraire hoeveelheid groepen is verdeeld,
laten we zeggen p,
en dat we deze groepen als
V1,...,
Vp noteren.
Een bepaald net n
i kan nu punten uit meerdere van deze groepen bevatten;
hoeveel precies noemen we de
verbindingsgraad,
en noteren we met λ
i.
De som van de verbindingsgraden van alle netten
geeft ons een idee van hoe goed de punten uit de verschillende groepen met elkaar verbonden zijn.
Over het algemeen maakt het ons niet uit als een net precies verbonden is met 1 groep;
dat betekent namelijk dat de bijbehorende berekeningen compleet lokaal zijn aan die ene groep.
Ook is het ene net meestal niet belangrijker dan een andere,
en dus gebruiken we de volgende kostenfunctie:
Dit wordt ook wel de (λ−1)-metriek genoemd.
De perfecte situatie correspondeert met een uitkomst 0 van bovenstaande som,
dat wil zeggen,
wanneer het probleem uiteenvalt in kleine stukjes die totaal niets met elkaar te maken hebben.
Dit gebeurde bijvoorbeeld bij het voorbeeld van steden als punten en provincies als netten;
het groeperen van punten aan de hand van provincies geeft een perfecte partitionering,
als er tenminste evenveel steden zijn in elke provincie.
Indien niet,
is het geen eerlijke verdeling,
en moeten er bij partitionering concessies gemaakt worden waardoor de kosten hoger uit zullen vallen.
Partitionering en herordening
De nieuwe bijdragen van dit proefschrift zitten niet zozeer in technieken ter verbetering van partitionering.
Er wordt ervan uitgegaan dat een manier om een goede partitionering te vinden al beschikbaar is,
en bovendien aan bepaalde voorwaarden voldoet.
Op basis van het resultaat van zo'n partitioneerder wordt herordening toegepast,
en dat is waar dit proefschrift iets aan wil toevoegen in Hoofdstuk 1 en 2.
Om de resultaten kracht bij te zetten is de herordeningsmethode wel toegevoegd aan het Utrechtse softwarepakket
`Mondriaan',
welk voorheen alleen geschikt was voor het partitioneren van ijle matrices en hypergrafen.
De herordeningsmethode werkt door de link tussen matrices en hypergrafen verder uit te buiten.
Niet alleen wordt de partitionering van de punten (
V) van de hypergraaf gebruikt,
maar ook de informatie van de netten (
N) wordt betrokken bij het terugvertalen van hypergraaf naar matrix.
Als we wederom aannemen dat
V in twee groepen is verdeeld,
namelijk
VL en
VR,
dan kunnen we
N in drie groepen verdelen:
een groep
N+ met netten die alleen iets te maken hebben met punten in
VL,
een groep
N− met netten alleen in
VR,
en de groep
Nc met overgebleven netten met verbindingsgraad 2.
Dit betekent dat onze oorspronkelijke matrix A na partitionering kan worden ingedeeld als:
ofwel,
alle niet-nullen in
VL verplaatsen we naar links,
die in
VR naar rechts,
en tegelijkertijd verplaatsen we rijen bevat in
N+ naar boven,
de rijen in
N− naar beneden,
en de resterende rijen in
Nc laten we in het midden.
De resulterende vorm van
~A na herordening,
ook hierboven afgebeeld,
is nieuw en noemen we de
Separated Block Diagonal (SBD) vorm,
of,
in goed Nederlands,
de `gescheiden blokdiagonaal'-vorm.
Dit omdat de submatrices (blokken) A
1 en A
4 hierboven op een diagonaal lijken te liggen,
gescheiden door een rij van matrices A
2 en A
3.
Waarom is deze vorm goed voor het probleem van ijle matrix-vector vermenigvuldiging?
Dit wordt duidelijk wanneer we y=Ax vervangen door
~y=
~A
~x,
met
~x,
~y op dezelfde manier geherordend als
~A.
Herinner dat A ijl is,
en dat A
1,...,A
4 dat dan ook zijn,
terwijl A en
~A even groot zijn;
dat wil zeggen,
A
1,...,A
4 zijn kleinere ijle matrices dan A maar bevatten samen dezelfde informatie als de originele A zelf.
De vermenigvuldiging wordt:
|
|
~
y
|
= |
~
A
|
|
~
x
| = |
⎛
⎜
⎜
⎜
⎝
|
|
⎞
⎟
⎟
⎟
⎠
|
| ⎛
⎜
⎜
⎝
|
| ⎞
⎟
⎟
⎠
|
= | ⎛
⎜
⎜
⎜
⎝
|
| ⎞
⎟
⎟
⎟
⎠
|
. |
|
Het eerste wat opvalt is dat de uitkomst
~y uit drie delen bestaat (A
1x
1, A
2x
1+A
3x
2, en A
4x
2),
terwijl
~y hetzelfde is als de originele y,
maar in een andere volgorde.
Ook zijn x
1 en x
2 samen even groot als x (en ook gelijk, op herordening na),
maar de vermenigvuldiging op zowel x
1 en x
2 wordt alleen gebruikt op het middelste deel van
~y;
het eerste en het laatste deel gebruiken alleen x
1 of alleen x
2.
Met andere woorden zijn de berekeningen nu geconcentreerd in het bovenste deel of het onderste deel van
~x,
behalve wanneer het middelste deel A
2x
1+A
3x
2 wordt berekend.
En de hoogte van A
2 en A
3 is impliciet juist dat wat de partitioneerder minimaliseert met de (λ−1)-metriek (zie de vorige sectie).
Als het in tweeën splitsen van berekeningen (dat wil zeggen, rekenen met x
1 en x
2) al lijkt te helpen,
waarom zouden we dan stoppen met twee?
Inderdaad is het mogelijk een
~x te hebben die in 4 stukken is verdeeld,
door simpelweg dezelfde truuk toe te passen met A
1 en A
4.
In het hele herordeningsverhaal hierboven kunnen we namelijk A vervangen door A
1,
om zo een Separated Block Diagonal vorm van A
1 krijgen:
en evenzo voor A
4.
Deze manier van overnieuw toepassen heet
recursie.
Plakken we bovenstaand plaatje na recursie op A
1 en A
4 in het originele SBD-plaatje van
~A,
en hernoemen we de matrices met onderscheid tussen de diagonaalmatrices A
i en de scheidingsmatrices S
i,
dan krijgen we de volgende structuur:
|
|
~
A
|
= | ⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
|
| ⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
|
. |
|
En natuurlijk kunnen we doorgaan met recursie op de verschillende submatrices A
i,
totdat niet meer verder kan worden gegaan;
dat wil zeggen,
totdat alle rijen in een scheidingsmatrix zitten,
of totdat de submatrices zo klein zijn dat ze precies 1 kolom bevatten.
Door op deze manier recursie en partitionering te combineren,
kan de ijle matrix-vector vermenigvuldiging dus zo lokaal mogelijk worden gemaakt
zodat het goed werkt op computers met caches,
ongeacht de precieze grootte van die caches.
In die zin zijn we ons niet bewust van de cache,
of,
in goed Engels,
de herordeningsmethode is
cache-oblivious.
Ook heeft het minimaliseren van de kostenfunctie ∑
i:ni ∈ N(λ
i−1) nog een bijkomend voordeel,
naast dat het de verschillende scheidingsmatrices (S
i) rij-gewijs dun houdt:
het zorgt ervoor dat de SBD-structuur ook wordt nagestreefd binnen de rijen van scheidingsmatrices zelf.
Bovendien is er theoretisch,
gegeven een bepaalde cache,
een aantal recursiestappen aan te wijzen waarvoor de kostenfunctie exact aangeeft hoeveel elementen uit x er maximaal van buiten de cache moeten worden gehaald.
Ofwel,
het is aangetoond dat de kostenfunctie inderdaad de onnodige beweging van gegevens minimaliseert,
en dat terwijl het klassiek gezien de communicatie tijdens een parallelle ijle matrix-vector vermenigvuldiging minimaliseert.
In de praktijk zien herordeningen er als volgt uit (met telkens het origineel links en de geherordende matrix rechts):

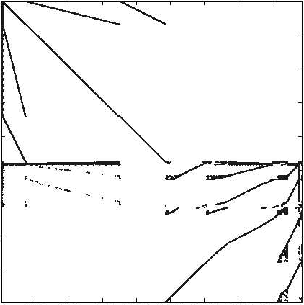
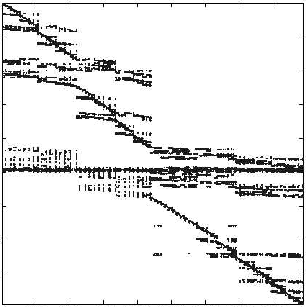
Een ijle matrix uit het toepassingsgebied van chip industrie, genaamd memplus. De originele structuur van de matrix staat links; resultaten na herordening in twee delen staat in het midden, en voor honderd delen rechts.



De rhpentium matrix, ook uit de chip industrie. Originele structuur links, resultaat na herordening in honderd delen in het midden, en voor vierhonderd delen rechts.
Dat de matrices er inderdaad in SBD-vorm uit zien is mooi,
maar wat is het effect op de daadwerkelijke ijle matrix-vector vermenigvuldiging?
Het proefschrift bevat veel experimenten op dit gebied,
maar voor deze uiteenzetting beperken we ons alleen tot onderstaande tabel.
Veel van de gebruikte matrices zijn overigens te vinden in de
ijle matrix verzameling van de Universiteit van Florida.
| Matrix | Natural | 1D | 1D & Blocking |
| fidap037 | 0.13 | | 0.13 | | (2) | 0.17 | | (2) |
| memplus | 0.32 | | 0.30 | | (2) | 0.35 | | (2) |
| rhpentium | 0.98 | | 0.75 | | (50) | 1.02 | | (5) |
| lhr34 | 1.71 | | 1.71 | | (10) | 1.76 | | (3) |
| nug30 | 6.37 | | 5.80 | | (2) | 6.48 | | (6) |
| s3dkt3m2 | 8.64 | | 8.62 | | (2) | 8.66 | | (2) |
| tbdlinux | 7.17 | | 6.53 | | (4) | 6.15 | | (2) |
| stanford | 22.0 | | 10.6 | | (9) | 10.3 | | (9) |
| stanford_berkeley | 24.6 | | 24.1 | | (3) | 23.8 | | (7) |
| cage14 | 111 | | 116 | | (8) | 113 | | (2) |
| wikipedia-2005 | 264 | | 179 | | (7) | 161 | | (9) |
| GL7d18 | 730 | | 452 | | (8) | 412 | | (9) |
| wikipedia-2006 | 819 | | 399 | | (9) | 383 | | (10) |
De duur voor een ijle matrix--vector vermenigvuldiging in milliseconden. Dertien matrices zijn getest; de snelheden in de meest linkse kolom geven de referentiesnelheiden voor standaardmethodes op de originele, niet-geherordende vorm van de matrix. De middelste kolom komt overeen met de methode die hier beschreven is; dit komt overeen met de technieken uit Hoofdstuk 1 van het proefschrift. Tussen haakjes staat in hoeveel delen is geherordend.
De laatste kolom betreft SBD herordeningen met achterliggende aanvullingen gepresenteerd in Hoofdstuk 2 van het proefschrift;
deze aanvullingen zullen in deze uiteenzetting helaas niet aan bod komen.
Twee-dimensionaal herordenen
De net uitgelegde herordeningsmethode kan worden uitgebreid zodat na herordening de zogenaamde
Doubly SBD-vorm tevoorschijn komt.
Deze ziet er na een splitsing in tweeën als volgt uit:
Wederom kan er recursief gewerkt worden op A
1 en A
2.
Het voordeel van deze vorm is dat dankzij introductie van een tweede dimensie
(er is nu ook een verticale kolom scheidingsmatrices,
in plaats van alleen een horizontale rij),
de rij-hoogte van S
{2,3,4} en de kolom-breedte van S
{1,3,5} kleiner kunnen worden gemaakt dan wanneer er alleen één van die richtingen beschikbaar was.
Om deze vorm in recursie te kunnen gebruiken,
is er echter meer dan alleen herordening nodig;
theoretisch is de vraag in welke volgorde de submatrices en scheidingsmatrices doorlopen moeten worden,
en praktisch is de vraag hoe de matrix opgeslagen moet worden in het computergeheugen.
Dit alles is het domein van Hoofdstuk 2,
en de resultaten verbeteren inderdaad die van de oorspronkelijke methode uit Hoofdstuk 1:
| Matrix | 2D Mondriaan | 2D finegrain |
| fidap037 | 0.127 | | (4) | 0.128 | | (7) |
| memplus | 0.306 | | (2) | 0.308 | | (2) |
| rhpentium | 0.736 | | (50) | 0.754 | | (50) |
| lhr34 | 1.566 | | (2) | 1.705 | | (10) |
| nug30 | 5.422 | | (3) | 5.931 | | (3) |
| s3dkt3m2 | 7.996 | | (3) | 8.640 | | (2) |
| tbdlinux | 6.254 | | (2) | 6.243 | | (2) |
| stanford | 9.86 | | (10) | 10.44 | | (9) |
| stanford_berkeley | 23.66 | | (2) | 24.02 | | (2) |
| cage14 | 109.5 | | (10) | 110.7 | | (2) |
| wikipedia-2005 | 119.4 | | (7) | 138.3 | | (9) |
| GL7d18 | 424.6 | | (10) | 422.7 | | (5) |
| wikipedia-2006 | 261.3 | | (9) | 346.7 | | (9) |
Zelfde tabel als de voorgaande, wederom met de tijden in milliseconden, maar nu voor de technieken behandeld in Hoofdstuk 2. Tussen 2D Mondriaan en 2D finegrain zit een verschil in hoe de DSBD-vormen recursief worden opgebouwd; dit zal in deze uiteenzetting helaas niet verder belicht worden.
Een andere oplossing
Het herordenen komt volgens bovenstaande dus uit op een methode die goed werkt ongeacht de specifieken van caches,
maar heeft wel de hulp van een ijle matrix partitioneerder nodig.
Hoofdstuk 3 behandelt echter een alternatief dat werkt vanuit een ander perspectief:
het veranderen van de volgorde waarin elementen uit een matrix betrokken worden in een matrix-vector vermenigvuldiging.
Tot nu toe hebben we impliciet aangenomen dat de volgorde rij-voor-rij is,
van boven naar beneden,
en binnen een rij van links naar rechts.
Laten we dit los,
dan kan het kiezen van een goede volgorde ervoor zorgen dat berekeningen lokaal blijven.
Een geschikte volgorde wordt gegeven door de Hilbert curve:
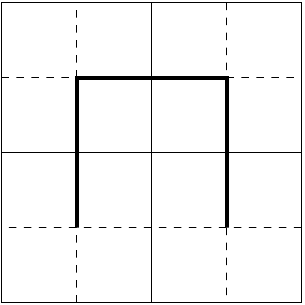
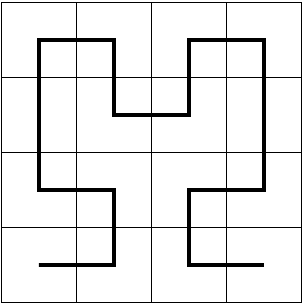
De Hilbert-curve op een 2-bij-2 matrix (links), en zijn verfijning voor een 4-bij-4 matrix (rechts).
In deze figuur wordt laten zien hoe een curve op een 2×2 matrix kan worden uitgebreid tot eentje op een 4×4 matrix.
Elk 2×2 kwadrant van die grotere matrix bevat echter een (geroteerde) versie van de originele curve op de 2×2 matrix;
er is dus een recept om elk kwadrant weer verder te verfijnen,
om zo een Hilbert curve op een 16×16 matrix te verkrijgen.
Wederom is een cruciaal ingrediënt recursie,
en hiermee gewapend kunnen arbitrair grote matrices ingetekend worden met een Hilbert curve.
De truuk is nu om de volgorde van deze curve te laten bepalen in welke volgorde niet-nullen behandeld worden.
Vanwege de recursieve manier waarop de curve gebouwd is,
zitten opeenvolgende niet-nullen in deze volgorde ook ruimtelijk dicht bijelkaar;
en dus worden er elementen uit x en y aangesproken die ook dicht bijelkaar zitten.
Deze methode vereist verder alleen de berekening van de plek van niet-nullen op de Hilbert curve,
een relatief veel simpelere berekening dan die partitionering met zich meebrengt.
Deze methode was niet nieuw,
echter was ze voorheen niet competitief vanwege de moeilijkheid hoe de niet-nullen in een arbitraire volgorde op te slaan.
De voor de hand liggende methode (sla voor elke niet-nul de waarde en positie op),
gebruikt noodgedwongen meer geheugen dan de standaard opslagmethode.
Als de matrix meer geheugen nodig heeft,
is er natuurlijk ook meer geheugenverkeer nodig om de vermenigvuldiging uit te voeren;
en hier ging het mis.
De extra lokaliteit werd teniet gedaan door het veroorzaakte extra verkeer.
In Hoofdstuk 3 van het proefschrift wordt een nieuwe datastructuur beschreven die dit probleem deels oplost,
waardoor de methode met de Hilbert curve opeens wel competitief is geworden.
Deze aangepaste datastructuur kan overigens ook worden gecombineerd met de twee-dimensionale herordeningsmethode uit Hoofdstuk 2.
Alhoewel dus sneller te prepareren en competitief gemaakt met de nieuwe datastructuur,
zijn de resultaten met deze methode niet zo sterk als wanneer gebruik wordt gemaakt van herordening;
zie de volgende tabellen.
| | | | | |
| Matrix | | CRS | ICRS | Hilbert | Extra tijd |
| stanford | | 22.15 | 27.52 | 18.48 | 832 |
| cont1_l | | 31.07 | 26.99 | 48.05 | 3084 |
| stanford-berkeley | | 26.05 | 24.52 | 34.29 | 3415 |
| Freescale1 | | 98.55 | 95.00 | 148.04 | 8913 |
| wikipedia-2005 | | 368.36 | 387.39 | 250.3 | 5850 |
| cage14 | | 116.44 | 110.69 | 140.20 | 12095 |
| GL7d18 | | 716.32 | 824.32 | 452.89 | 10064 |
| wikipedia-2006 | | 823.53 | 879.53 | 550.00 | 11814 |
| wikipedia-2007 | | 1033.95 | 1124.02 | 591.08 | 14753 |
Resultaten voor versnelling van de ijle matrix--vector vermenigvuldiging door aanpassing van de volgorde van verwerking van niet-nullen middels de Hilbert curve. Alle getallen staan in milliseconden; CRS is de standaardmethode voor opslag van ijle matrices, en ICRS is een variant daarop. De extra tijd geeft weer hoeveel meer moeite het kost de Hilbert-curve te gebruiken ten opzichte van het gebruik van CRS.
Het verdient wel op te merken dat de methodes van matrixherordening en de hier besproken methode van verandering van de volgorde van niet-nullen,
elkaar totaal niet uitsluiten;
er is niets op tegen eerst een matrix te herordenen,
om vervolgens aan de slag te gaan met de Hilbert curve.
De voorheen behandelde hoofdstukken bevinden zich in een ander deel dan Hoofdstuk 4 en 5.
Dit heeft een eenvoudige reden:
tot nu toe is de ijle matrix-vector vermenigvuldiging behandeld als zijnde één enkele berekening,
ofwel,
een
sequentiële berekening.
Bij herordening wordt echter gebruik gemaakt van partitionering,
welk oorspronkelijk parallel rekenen mogelijk maakte;
een logische vraag is of we de gevonden methodes niet kunnen combineren met een parallelle vermenigvuldiging,
en dit is waar Deel 2 van het proefschrift zich mee bezig houdt.
Een eerste vraag van de lezer is wellicht wat parallellisatie precies inhoudt.
Simpel gezegd is het precies het verschil tussen één persoon een taak geven,
of die taak geven aan een groep personen.
Zijn er vier muren te beschilderen en wordt dit gedaan door een enkele schilder,
dan is dat een sequentiële oplossing.
Wordt de taak volbracht door meerdere schilders,
dan noemen we dat een parallelle oplossing.
In de wereld van computerberekeningen zijn er,
net zoals in het echte leven,
triviale taken en moeilijke taken wat betreft parallellisatie.
In het geval van vier schilders bijvoorbeeld,
is er niet veel fantasie nodig om een initiële taakverdeling te bedenken:
elke schilder schildert één voorafbepaalde muur.
Er rijst dan wel direct de vraag wat er gebeurt als de muren niet even groot zijn;
als de schilders met de kleinere muren eerder naar huis gaan en zij hun collega's met grotere muren alleen door laten werken,
duurt het schilderen in zijn geheel langer dan wanneer samen zou worden gewerkt aan de overgebleven muren.
We zeggen dan dat de parallellisatie slecht gebalanceerd is,
want ideaal willen we dat de benodigde schildertijd precies gelijk is aan de sequentiële tijd
(de tijd die één schilder nodig gehad zou hebben),
gedeeld door het aantal schilders.
Computers zijn niet zo intelligent als mensen,
en als de taak ook maar een beetje complex is,
dan is parallellisatie niet makkelijk.
Elke stap moet expliciet duidelijk gemaakt worden aan de computer:
hoe moet het probleem initiëel verdeeld worden,
hoeveel werkers moet ik tegelijkertijd opstarten,
wat als één van die werkers al klaar is,
en hoe combineer ik de individuele resultaten van al die werkers tot het eigenlijke eindresultaat?
Ook zijn er nog steeds behoorlijk wat verschillende computers op de markt,
die allemaal hun eigen communicatiemiddelen tussen werkers beschikbaar stellen;
moeten geparallelliseerde taken specifiek voor een bepaalde computer geschreven worden?
Zelfs lastigere vragen doemen op wanneer het kan gebeuren dat werkers `crashen';
vergelijk het met een schilder die plotseling ziek wordt en naar huis gaat.
Allicht nog kwalijker kan het in de toekomst ook nog zo zijn dat een computerwerker zijn berekening niet goed doet,
en foute antwoorden geeft;
zeg maar als een schilder die met de verkeerde pot verf aan de gang is gegaan.
Computers,
inclusief de voorziene toekomstige architecturen,
zijn niet creatief en initiatiefrijk genoeg om werk van hun zieke collega over te nemen,
of om zelf achter de fout te komen
en vervolgens dan maar de goede pot verf te halen om overnieuw te beginnen;
al dat soort acties moeten expliciet geprogrammeerd worden.
Bulk Synchronous Parallel en multicore rekenen
Of toch niet?
Sommige van deze problemen komen al langer voor,
en men heeft daar oplossingen voor bedacht in de vorm van
bridging models;
modellen die het idee van een parallelle computer (eentje die meerdere werkers op een enkele taak kan zetten),
abstraheren tot een theoretisch apparaat dat iedereen kan programmeren.
Vervolgens stellen computerontwikkelaars software-bibliotheken beschikbaar die programma's voor het theoretische apparaat kunnen vertalen naar code die werkt op de computers die zij verkopen.
Klassieke voorbeelden van zulke modellen en bibliotheken zijn
Message Passing Interface (MPI) en
Bulk Synchronous Parallel (BSP),
en richten zich voornamelijk op supercomputers die bestaan uit meerdere fysieke processoren,
met elkaar verbonden middels een gespecialiseerd snel netwerk.
Het parallelliseren van een berekening begint dan ook meestal met het kiezen van een bridging model,
en vervolgens het nadenken en implementeren van een oplossing die snel zou moeten werken binnen dat model.
In het geval van programmeren in BSP,
waar in Hoofdstuk 4 van wordt uitgegaan,
zijn parallelle programma's opgedeeld in superstappen,
en voert elke werker hetzelfde parallelle programma uit.
In een superstap kan een werker alleen berekeningen uitvoeren met lokaal beschikbare data;
het kan niet zelf bij de gegevens van andere werkers komen,
noch kan het communiceren met andere werkers.
Tussen superstappen in wordt
gesynchroniseerd;
dat wil zeggen,
alle werkers wachten op elkaar zodat tegelijkertijd kan worden begonnen aan de volgende superstap.
Het is alleen toegestaan dat tussen de superstappen in wordt gecommuniceerd.
De opdrachten daartoe kunnen echter alleen tijdens de superstap worden gegeven.
Data van andere werkers kunnen dus tijdens een superstap opgevraagd worden
(of andersom, data kan aan andere werkers verzonden worden),
maar deze communicatie wordt pas later uitgevoerd en de data is pas op de opgegeven bestemming beschikbaar wanneer de volgende superstap begint.
Dit gaat expliciet uit van een parallelle computer met
gedistribueerd geheugen;
werkers hebben hun eigen lokale geheugen en communicatie tussen superstappen in gebeurt via een netwerk.
Een groot voordeel van deze opzet is dat BSP de benodigde parallelle rekentijd kan
voorspellen.
Dit komt omdat de snelheid van werkers bekend is,
alsook de snelheid van het netwerk (hoe lang duurt het om zus en zoveel te versturen).
Bovendien is de tijd nodig om te synchroniseren (zonder communicatie) meetbaar.
Als vervolgens de maximale hoeveelheid berekeningen van de verschillende werkers per superstap bekend is,
en als per werker ook bekend is wat de maximum hoeveelheid verstuurde of ontvangen data is,
dan zijn alle ingrediënten bekend om de verwachte tijd uit te rekenen.
Tegenwoordig zijn de
multicore processoren wijd verspreid.
Deze combineren meerdere `cores' (werkers) op een enkele processor;
een gemiddelde computer heeft tegenwoordig twee cores,
en de wat duurdere varianten hebben er vier of zes op één chip.
Het grootste verschil met wat hierboven is beschreven,
is dat omdat de werkers op één processor zitten,
ze ook de geheugenstructuur delen.
Hetzelfde globale geheugen wordt gedeeld,
net zoals de caches die tussen de processor en dat geheugen zitten.
Dit delen van caches maakt het interessant te bekijken wat de wisselwerking is met de technieken uit het eerste deel,
die ten doel hadden optimaal gebruik te maken van de caches.
Bibliotheken specifiek voor gedeeld-geheugen parallellisme bestaan al geruime tijd;
bekende voorbeelden zijn OpenMP en POSIX Threads (PThreads).
Hoofdstuk 4 houdt zich echter eerst bezig met het brengen van het oorspronkelijke BSP model naar parallelle computers met gedeeld geheugen.
In dit model wordt nog steeds aangenomen dat werkers verbonden zijn met het netwerk,
alleen is het netwerk hier nu synoniem met de caches die alle cores met elkaar verbinden;
dat wil zeggen, het eigenlijke theoretische model is niet veranderd.
Een versimpeling komt wel tevoorschijn bij de bijbehorende BSP software-bibliotheek;
communicatie over dat netwerk is dan namelijk synoniem met het kopiëren van data,
in plaats van codering en verzending over een netwerk.
Omgekeerd maakt de gedeeld-geheugen architectuur het lezen van gegevens,
ongeacht van welke werker deze gegevens zijn,
veel makkelijker.
Op dit gebied is de standaard BSP bibliotheek dan ook uitgebreid,
en een concept software-bibliotheek genaamd
MulticoreBSP is tegelijkertijd met dit proefschrift ontwikkeld.
IJle matrix-vector vermenigvuldiging in BSP
Nu volgt een korte beschrijving van de parallelle implementatie van de ijle matrix-vector vermenigvuldiging in het BSP model.
Het werk dat hoort bij deze vermenigvuldiging wordt veroorzaakt door de niet-nullen in de matrix A;
elke niet-nul moet vermenigvuldigd worden met het juiste element uit x,
en de uitkomst daarvan moet opgeteld worden bij het juiste element uit y.
Dit betekent dat de niet-nullen verdeeld moeten worden over werkers,
en wel op een manier zodat de werkers elkaar zo min mogelijk voor de voeten lopen door hetzelfde element uit x op te vragen of te schrijven naar hetzelfde element uit y.
Zoals eerder opgemerkt worden zulke verdelingen gevonden door ijle matrix partitioneerders zoals Mondriaan,
maar wordt er in dit proefschrift niet ingegaan op de technieken van partitioneerders,
en wordt simpelweg verondersteld dat externe partitioneerders beschikbaar zijn (en goed werken).
Het klassieke parallelle algoritme partitioneert niet alleen de matrix A,
maar ook de vectoren x en y.
Dit is vanwege
schaalbaarheid;
een reden voor parallellisatie is niet alleen snelheidswinst,
maar soms ook dat het verdelen over meerdere werkers een extreem groot probleem behandelbaar maakt
(een probleem kan simpelweg te groot zijn voor een enkele computer).
Om deze reden moet
alle benodigde data dan ook daadwerkelijk verdeeld worden over alle werkers,
in dit geval de matrix inclusief de betrokken vectoren.
Bovendien zou er erg veel communicatie nodig zijn als elke werker beide vectoren accuraat bij moet blijven houden.
Alle niet-nullen voor een bepaalde werker worden gegroepeerd in een lokale matrix
―A,
en gelijk zo met de lokale versies
―x en
―y van x en y,
respectievelijk.
De grootte van lokale objecten
―A,
―x en
―y is kleiner dan of gelijk aan de grootte van de originele matrix en vectoren.
Het is nu verleidelijk te zeggen dat elke werker
―y=
―A
―x moet uitrekenen en dat is alles;
maar niets is minder waar.
Omdat x en y verdeeld zijn,
is het mogelijk dat niet-nullen in
―A corresponderen met elementen uit x die niet lokaal zijn (niet in
―x zitten),
maar juist bij een andere werker aanwezig zijn.
Evenzo kunnen er niet-nullen in
―A zitten die moeten communiceren met elementen uit y aanwezig bij andere werkers.
Het standaard BSP algoritme haalt derhalve in de eerste superstap alle lokaal nodige elementen uit x vanuit de andere processoren.
In de volgende superstap zijn deze elementen beschikbaar,
en kan rij-voor-rij de daadwerkelijke matrix-vector vermenigvuldiging uitgevoerd worden.
Als een rij niet lokaal is,
dat wil zeggen,
als de uitkomst bij een element van y moet worden opgeteld dat niet aanwezig is in
―y,
dan wordt deze uitkomst doorgestuurd naar de werker die het element wel heeft.
Hierna wordt weer gesynchroniseerd,
en in de laatste superstap worden de binnenkomende bijdragen voor
―y opgeteld;
het is immers net zo goed mogelijk dat andere werkers niet-nullen in een rij hadden die corresponderen met elementen in onze
―y.
Op systemen met gedeeld geheugen is het opvragen van niet-lokale gegevens uit x wel direct mogelijk,
zonder superstap,
maar ook hier gebeurt zoiets liever met mate.
Dit omdat het inefficiënt cachegebruik waarschijnlijk maakt:
cache-gebruik zou goed zijn juist wanneer alle werkers hetzelfde element op hetzelfde moment opvragen,
maar om dit te garanderen moeten de werkers constant communiceren om ervoor te zorgen dat ze in hetzelfde tempo werken (ofwel, constant synchroniseren).
Zoiets zou betekenen dat ze meer met elkaar praten dan dat ze daadwerkelijk werk verzetten.
Voor y is hetzelfde overigens totaal
niet mogelijk.
Stel dat element y
3 uit y op het moment gelijk is aan 0.5,
en dat een werker het getal 3.5 bij y
3 wil optellen terwijl er tegelijkertijd een tweede werker is die 5 wil optellen bij y
3.
De eerste werker telt lokaal 3.5 bij 0.5 op en komt uit op 4,
en schrijft dat terug naar y
3.
De tweede werker is zich, net zo min als de eerste werker, van geen kwaad bewust en doet hetzelfde met 5,
en schrijft dan 5.5 terug naar y
3.
Beide schrijfopdrachten racen terug naar het globale geheugen waar de vector y staat,
en wie als laatste aankomt wint (het is ook goed mogelijk dat deze fout door het systeem gedetecteerd wordt,
wat doorgaans de hele parallelle berekening afbreekt met een foutmelding).
De waarde van y
3 wordt dus 5.5 of 4,
beide ongelijk aan het eigenlijke antwoord (9).
Dit is dan ook de reden dat MulticoreBSP het lezen van data van een andere werker wel toestaat,
maar het schrijven daartoe niet.
Al met al is het ijle matrix-vector vermenigvuldigingsalgoritme voor systemen met gedeeld geheugen hetzelfde als het algoritme voor gedistribueerd geheugen wat hierboven beschreven is,
behalve dat niet-lokale elementen uit x direct kunnen worden uitgelezen en er dus een superstap minder nodig is.
Wegens efficiënt cachegebruik met betrekking tot niet-lokale elementen uit x,
is een goede partitionering in beide richtingen (x en y) nog steeds belangrijk.
Herordening en parallellisme op systemen met gedeeld geheugen
Zoals eerder opgemerkt worden ook caches gedeeld tussen werkers wanneer multicore systemen gebruikt worden.
Hoofdstuk 5 combineert de inzichten van al het voorgaande om een cache-efficiënte parallelle vermenigvuldiging te bewerkstelligen.
De methode daar gepresenteerd kan als volgt geschetst worden.
Stel dat we de beschikking hebben over twee cores,
en dat de matrix in doubly SBD-vorm is gebracht dankzij de technieken ontwikkeld in Deel I:
Met de vorige sectie in gedachten,
en onder aanname van geschikte vector-distributies voor x en y,
zien we dat A
1 en A
2 corresponderen met de niet-nullen die werkers 1 en 2 compleet onafhankelijk van elkaar kunnen behandelen.
S
1 correspondeert met niet-nullen waarvoor werker 1
mogelijk een element uit x van werker 2 moet halen,
en evenzo voor S
5 maar met de rollen van de twee werkers omgedraaid.
S
2 correspondeert met niet-nullen waarvoor werker 1 mogelijk bijdragen aan een element uit y naar werker 2 moet sturen,
en wederom omgekeerd hetzelfde voor S
4.
S
3 heeft de hoofdprijs;
hier moeten werker 1 en 2 zowel mogelijk elementen van x van de andere werker opvragen,
alsook mogelijk bijdragen aan y sturen naar de andere werker.
Willen we gebruik maken van de herordening,
dan is het makkelijker te veronderstellen dat er geen lokale versies van
~A, x en y gevormd worden,
maar dat alle werkers op het origineel opereren.
Dit betekent dat we buiten het BSP model om werken;
de experimentele software ontwikkeld bij dit hoofdstuk is dan ook geschreven in PThreads in plaats van met MulticoreBSP.
In de vorige sectie is beargumenteerd dat het lezen van elementen van x bij andere werkers toegestaan is voor systemen met gedeeld geheugen.
Dit betekent dat het voor werkers toegestaan is om zonder meer te lezen uit een globale x,
omdat de herordening gebaseerd is op de partitionering.
S
{1,5} lijken zich in die zin automatisch goed te gedragen,
maar S
{2,3,4} zijn lastiger aangezien onder geen voorwaarde meerdere werkers naar hetzelfde deel van y mogen schrijven.
Dit is in het huidige hoofdstuk opgelost door meervoudige synchronisatie;
eerst wordt alleen werker 1 toegestaan op S
{2,3,4} te werken,
en daarna, dus na synchronisatie, is werker 2 aan de beurt.
Deze methode is verder verfijnd door de rijen van S
{2,3,4} van te voren in tweeën te verdelen,
zodat beide werkers op (ongeveer) de helft van de rijen van deze scheidingsmatrices kunnen opereren.
Na synchronisatie wisselen de werkers van helft om de berekening af te maken.
Op deze manier is de werkbalans optimaal;
in de voorgaande versie zou telkens één werker louter toekijken hoe de ander aan de slag gaat,
terwijl ze nu beiden ongeveer evenveel te doen hebben.
Het enige nadeel is dat het aantal synchronisatiestappen proportioneel is aan het aantal werkers.
Hoe meer werkers,
hoe meer tijd er verloren gaat aan synchronisaties.
Wil deze methode aantrekkelijk blijven,
dan moet de grootte van de te vermenigvuldigen matrix dus meeschalen met het aantal werkers.
Net zoals bij Hoofdstuk 1 en 2 is het mogelijk meer te halen uit deze methode door gebruik te maken van recursie.
Ook al zouden er alleen twee werkers beschikbaar zijn,
het recursief opdelen van A
1 en A
2 zou voor beter cache-gebruik van die twee werkers moeten zorgen,
omdat berekeningen van beide werkers lokaler worden in x en y.
Samenvattend is de truuk om het aantal partities dus hoger te nemen dan het aantal beschikbare werkers,
zodat elke werker de SBD-vorm individueel kan uitbuiten,
terwijl op hoger niveau de werkers elkaar dankzij de partitioneerder zo min mogelijk voor de voeten lopen wat betreft de elementen die gedeeld moeten worden tussen meerdere werkers.
Resultaten van parallelle methoden
Resultaten van parallellisatie met MulticoreBSP en die van de combinatie met herordening in PThreads zijn te vinden in de volgende twee tabellen.
| | Intel Q6600 | AMD 945e |
| Matrix | p=2 | p=3 | p=4 | p=2 | p=3 | p=4 |
| west0497 | 0.61 | 0.69 | 0.59 | 0.97 | 1.08 | 0.54 |
| fidap037 | 0.27 | 0.25 | 0.19 | 0.41 | 0.26 | 0.22 |
| s3rmt3m3 | 0.28 | 0.23 | 0.34 | 0.44 | 0.32 | 0.29 |
| memplus | 0.96 | 0.35 | 0.32 | 0.95 | 0.48 | 0.37 |
| cavity17 | 0.26 | 0.24 | 0.18 | 0.30 | 0.30 | 0.25 |
| bcsstk17 | 0.96 | 0.41 | 1.18 | 1.20 | 0.45 | 0.78 |
| lhr34 | 1.22 | 1.08 | 0.53 | 1.17 | 1.77 | 0.55 |
| bcsstk32 | 0.73 | 0.89 | 0.87 | 1.04 | 0.99 | 1.20 |
| nug30 | 0.69 | 0.64 | 0.46 | 0.74 | 0.75 | 0.59 |
| s3dkt3m2 | 1.20 | 1.09 | 1.26 | 1.46 | 1.29 | 2.33 |
| tbdlinux | 1.20 | 0.96 | 0.87 | 1.52 | 1.23 | 1.46 |
| stanford | 1.72 | 1.79 | 1.98 | 1.46 | 1.92 | 1.93 |
| stan-ber | 1.22 | 1.25 | 1.26 | 1.51 | 1.79 | 1.82 |
| cage14 | 0.85 | 0.93 | 0.78 | 1.14 | 1.46 | 1.34 |
| wikipedia-2005 | 1.97 | 2.31 | 2.21 | 2.33 | 2.68 | 3.34 |
| wikipedia-2006 | 1.83 | 2.06 | 2.17 | 1.38 | 2.17 | 2.00
|
Resultaat van de ijle matrix--vector vermenigvuldiging in MulticoreBSP. De getallen geven hier de speedup aan; dat wil zeggen, hoeveel keer sneller het parallele algoritme is dan wanneer uitgevoerd met alleen 1 werker. Hier zijn twee architecturen weergegeven: de Intel Core2 Q6600 en de AMD Phenom II 945e. Beide zijn quad-core processoren waar elk van de vier cores een snelheid heeft van 2.4GHz of 3.0GHz, respectievelijk.
De combinatie met herordening is minder uitgebreid getest,
met de resultaten op twee architecturen en twee voorbeeldmatrices weergegeven in de volgende tabel:
| | Intel Core 2 Q6600 |
| s3dkt3m2 | t\p | 4 | 16 | 32 | 64 |
| 1 | 17 | 16 | 18 | 17 |
| 2 | 17 | 16 | 18 | 17 |
| 4 | 20 | 18 | 22 | 21 |
| |
| |
| GL7d18 | t\p | 4 | 16 | 32 | 64 |
| 1 | 906 | 633 | 492 | 486 |
| 2 | 718 | 347 | 345 | 285 |
| 4 | 583 | 491 | 398 | 385
|
|
| | AMD Phenom II 945e |
| t\p | 4 | 16 | 32 | 64 |
| 1 | 11 | 11 | 14 | 11 |
| 2 | 8 | 7 | 9 | 8 |
| 4 | 6 | 7 | 6 | 6 |
| |
| |
| t\p | 4 | 16 | 32 | 64 |
| 1 | 482 | 373 | 352 | 372 |
| 2 | 333 | 376 | 236 | 357 |
| 4 | 250 | 200 | 199 | 237 |
|
Snelheden van ijle matrix--vector vermenigvuldiging voor een parallelle implementatie met herordening. Resultaten zijn in milliseconden. Het aantal t daadwerkelijk gebruikte werkers op een processor staat verticaal gegeven; het aantal delen p voor herordening staan horizontaal gegeven.
Het verdient nog een opmerking dat de MulticoreBSP software-bibliotheek zich niet beperkt tot de ijle matrix-vector vermenigvuldiging alleen;
ook oplossingen van andere problemen zijn geïmplementeerd en onderzocht op efficiëntie.
Deze andere problemen zijn het berekenen van het inwendig product van twee vectoren,
de snelle Fouriertransformatie (zoals ook gebruikt in compressie van muziek en beeld),
en LU decompositie (welke werkt op volle matrices, in tegenstelling tot ijle matrices).
Hoofdstuk 4 zet alle resultaten verkregen met deze toepassingen uiteen.
De combinatie van resultaten laat zien dat MulticoreBSP,
inclusief de uitbreiding op de standaard BSP bibliotheken,
inderdaad voor goede parallellisatie op huidige multicore computers kan zorgen.










